4 Regressão Linear Simples
Análise linear simples estuda a relação linear entre duas variáveis quantitativas. Sendo uma denominada de variável dependente e a outra de variável indenpendente. Essa análise é realizada a partir de dois pontos de vista diferentes:
regressão \(\rightarrow\) que expressa a forma da relação linear entre as duas variáveis e;
correlação \(\rightarrow\) que quantifica a força desse relacionamento.
Essa relação é representada por um modelo matemático, i.e., por uma equação que associará a variável explicada à variável explicativa. A representação matemática dessa associação é a seguinte:
\[\begin{equation} y = \beta_0 + \beta_1 x + \mu \tag{4.1} \end{equation}\]
em que:
\(y \rightarrow\) é a variável explicada ou dependente que será calculada e, portanto, é aleatória;
\(\beta_0\) e \(\beta_1 \rightarrow\) são os parâmetros desconhecidos do modelo que serão calculados. Quando se está trabalhando com a população diz-se que essas são as estimativas, no entanto, se está trabalhando com uma amostra diz-se que essas são os estimadores dos verdadeiros valores.
\(x \rightarrow\) é a variável explicativa ou independente medida sem erro, i.e., sem aleatoriedade e;
\(\mu \rightarrow\) é a variável aleatória residual na qual as outras variáveis que influenciam o comportamento da variável dependente \(y\), e que não foram incluídas no modelo matemático, são encontradas \(x\). Ou seja, são influências na variável explicada \(y\) que não podem ser explicadas linearmente pelo comportamento da variável explicativa.
Exemplo 3.1: A Tabela \(I.1\) do livro Econometria Básica, tradução da \(5ª\) edição, de Gujarati and Porter (2011, 30) será usada nesse exemplo.
## Exemplo:
## criando um data.frame com os dados da Tabela I.1
pers_con <- data.frame(
year = c(1960, 1961, 1962, 1963, 1964, 1965, 1966, 1967, 1968, 1969,
1970, 1971, 1972, 1973, 1974, 1975, 1975, 1977, 1978, 1979,
1980, 1981, 1982, 1983, 1984, 1985, 1986, 1987, 1988, 1989,
1990, 1991, 1992, 1993, 1994, 1995, 1996, 1997, 1998, 1999,
2000, 2001, 2002, 2003, 2004, 2005),
ecp = c(1597.4, 1630.3, 1711.1, 1781.6, 1888.4, 2007.7, 2121.8, 2185.0,
2310.5, 2396.4, 2451.9, 2545.5, 2701.3, 2833.8, 2812.3, 2876.9,
3035.5, 3164.1, 3303.1, 3383.4, 3374.1, 3422.2, 3470.3, 3668.6,
3863.3, 4064.0, 4228.9, 4369.8, 4546.9, 4675.0, 4770.3, 4778.4,
4934.8, 5099.8, 5290.7, 5433.5, 5619.4, 5831.8, 6125.8, 6438.6,
6739.4, 6910.4, 7099.3, 7259.3, 7577.1, 7841.2),
gdp = c(2501.8, 2560.0, 2715.2, 2834.0, 2998.6, 3191.1, 3399.1, 3484.6,
3652.7, 3765.4, 3771.9, 3898.6, 4105.0, 4341.5, 4319.6, 4311.2,
4540.9, 4750.5, 5015.0, 5173.4, 5161.7, 5291.7, 5189.3, 5423.8,
5813.6, 6053.7, 6263.6, 6475.1, 6742.7, 6981.4, 7112.5, 7100.5,
7336.6, 7532.7, 7835.5, 8031.7, 8328.9, 8703.5, 9066.9, 9470.3,
9817.0, 9890.7, 10048.8, 10301.0, 10703.5, 11048.6)
)
## chamando o data.frame criado
pers_con## year ecp gdp
## 1 1960 1597.4 2501.8
## 2 1961 1630.3 2560.0
## 3 1962 1711.1 2715.2
## 4 1963 1781.6 2834.0
## 5 1964 1888.4 2998.6
## 6 1965 2007.7 3191.1
## 7 1966 2121.8 3399.1
## 8 1967 2185.0 3484.6
## 9 1968 2310.5 3652.7
## 10 1969 2396.4 3765.4
## 11 1970 2451.9 3771.9
## 12 1971 2545.5 3898.6
## 13 1972 2701.3 4105.0
## 14 1973 2833.8 4341.5
## 15 1974 2812.3 4319.6
## 16 1975 2876.9 4311.2
## 17 1975 3035.5 4540.9
## 18 1977 3164.1 4750.5
## 19 1978 3303.1 5015.0
## 20 1979 3383.4 5173.4
## 21 1980 3374.1 5161.7
## 22 1981 3422.2 5291.7
## 23 1982 3470.3 5189.3
## 24 1983 3668.6 5423.8
## 25 1984 3863.3 5813.6
## 26 1985 4064.0 6053.7
## 27 1986 4228.9 6263.6
## 28 1987 4369.8 6475.1
## 29 1988 4546.9 6742.7
## 30 1989 4675.0 6981.4
## 31 1990 4770.3 7112.5
## 32 1991 4778.4 7100.5
## 33 1992 4934.8 7336.6
## 34 1993 5099.8 7532.7
## 35 1994 5290.7 7835.5
## 36 1995 5433.5 8031.7
## 37 1996 5619.4 8328.9
## 38 1997 5831.8 8703.5
## 39 1998 6125.8 9066.9
## 40 1999 6438.6 9470.3
## 41 2000 6739.4 9817.0
## 42 2001 6910.4 9890.7
## 43 2002 7099.3 10048.8
## 44 2003 7259.3 10301.0
## 45 2004 7577.1 10703.5
## 46 2005 7841.2 11048.6## year ecp gdp
## Min. :1960 Min. :1597 Min. : 2502
## 1st Qu.:1971 1st Qu.:2584 1st Qu.: 3950
## Median :1982 Median :3569 Median : 5358
## Mean :1982 Mean :4047 Mean : 6023
## 3rd Qu.:1994 3rd Qu.:5243 3rd Qu.: 7760
## Max. :2005 Max. :7841 Max. :11049Todavia, no dia a dia os pesquisadores já possuem uma base em uma extensão qualquer, por exemplo .csv, e, então, precisam importar esses dados para o R. Para qualquer extensão o procedimento mais prático é utilizar o processo choose.files() que irá permitir ao usuário escolher o diretório em que se encontra a base. Por exemplo, para a extensão .csv o comando para importar uma base é da seguinte forma:
## importando uma base extensão `.csv' no R no padrão norte americano
pers_con <- read.csv(choose.files())Importante destacar que o comando read.csv funciona para bases .csv no padrão norte americano, i.e., as colunas são separadas por vírgula e a casa decimal é representada por ponto. Contudo, se a base .csv estiver no padrão brasileiro: colunas separadas por ponto e vírgula e a casa decimal é representada por vírgula o comando para importar tal base seria:
## importando uma base extensão `.csv' no R no padrão brasileiro
pers_con <- read.csv2(choose.files())Destaca-se que o comando summary reporta apenas algumas poucas estatísticas e, dessa forma, para realizar uma análise mais completa sobre as variáveis em estudo pode-se empregar o comando describe do pacote psych. Esse comando irá apresentar ao todo 11 estatísticas. A seguir apresenta-se cada uma delas:
\(mean \rightarrow\) representa a média aritmética da série;
\(sd \rightarrow\) representa o desvio padrão;
\(median \rightarrow\) representa a mediana da série;
\(trimmed \rightarrow\) representa a média trimmed (trimmed mean) ou média truncada;
\(mad \rightarrow\) representa o desvio absoluto mediano (da mediana);
\(min \rightarrow\) representa o valor mínimo;
\(max \rightarrow\) representa o valor máximo;
\(range \rightarrow\) representa o intervalo entre o valor mínimo e o valor máximo;
\(skew \rightarrow\) representa a assimetria da série. Um valor igual a zero indica que a série é perfeitamente simétrica. Por sua vez, quanto mais distante de zero, mais assimétrica será a série;
\(kurtosis \rightarrow\) representa o achatamento dos dados da série em relação à curva da distribuição normal (ou de Gauss). Para uma série normal esse valor é igual a \(0\). Séries com esse valor são denominadas de mesocúrtica. Para valores maiores (\(> 0\)), então a série em questão é mais alta (afunilada) e concentrada do que a distribuição normal. Diz-se que essa série é leptocúrtica. Já para valores menores (\(< 0\)) a série é mais achatada do que a distribuição normal. Diz-se que essa série é platicúrtica. e;
\(se \rightarrow\) representa o erro-padrão da série.
Para exemplificar o comando describe do pacote psych a seguir utiliza-se a variável gdp do data.frame pers_con e, a partir das estatísticas descritivas reportadas pode-se identificar se a variável gdp possui uma distribuição normal.
## chamando o pacote `psych'
library(psych)
## obtendo as estatísticas descritivas para a variável `gdp' do data.frame `pers_con'
describe(pers_con$gdp)## vars n mean sd median trimmed mad min max range skew
## X1 1 46 6022.94 2479.29 5357.75 5903.75 2592.7 2501.8 11048.6 8546.8 0.42
## kurtosis se
## X1 -1.04 365.554.1 Teste para normalidade Jarque-Bera e Shapiro-test
Para confirmar se a série possui uma distribuição normal ou não aplica-se o teste Jarque-Bera para normalidade cujo o procedimento se dá através da comparação do valor da kurtosis e skewness. Para realizar esse teste utiliza-se o comando jarque.bera.test do pacote tseries.
## chamando o pacote `tseries'
library(tseries)
## teste Jarque-Bera para normalidade da variável `gdp' do data.frame `pers_con'
jarque.bera.test(pers_con$gdp)##
## Jarque Bera Test
##
## data: pers_con$gdp
## X-squared = 3.1944, df = 2, p-value = 0.2025De posse do resultado do teste Jarque-Bera para normalidade não se rejeita a hipótese de normalidade se o valor p-value for maior do que o nível de significância escolhido. Para o exemplo, nota-se que para os níveis de significância padrão (\(1\%, 5\%\) e \(10\%\)) não se rejeita a hipótese de normalidade, i.e., a variável gdp possui uma distribuição aproximadamente normal uma vez que o p-value é maior do que aqueles níveis de significância.
Outro teste para normalidade seria o Shapiro test cuja hipótese nula é: a série em questão é normalmente distribuída.
##
## Shapiro-Wilk normality test
##
## data: pers_con$gdp
## W = 0.94175, p-value = 0.02276O resultado desse teste ratifica o resultado do teste Jarque-Bera nos níveis de significância (\(5\%\) e \(10\%\)), i.e., a série gdp possui uma distribuição aproximadamente normal uma vez que a esses níveis não se rejeita a hipótese nula de uma série normalmente distribuída.
Também pode-se “plotar” um histograma da série para uma análise visual para normalidade. A seguir, plota-se o histograma para a série gdp do data.frame pers_con e adicionam-se a curva normal (linha azul) e a curva para a série em questão, gdp (linha vermelha). Note que a linha em vermelha se aproxima de uma distribuição normal.
## plotando o histograma para a série `gdp' do data.frame `pers_con'
hist(pers_con$gdp, main = "Histograma para a série GDP", xlim = c(0, 14000),
ylim = c(0.00000, 0.00020), xlab = "GDP", col = "gray", probability = TRUE)
## adicionando a curva para análise visual de normalidade
curve(dnorm(x, mean = mean(pers_con$gdp), sd = sd(pers_con$gdp)), col = "darkblue",
lwd = 2, add = TRUE)
lines(density(pers_con$gdp), col = "red", lwd = 2)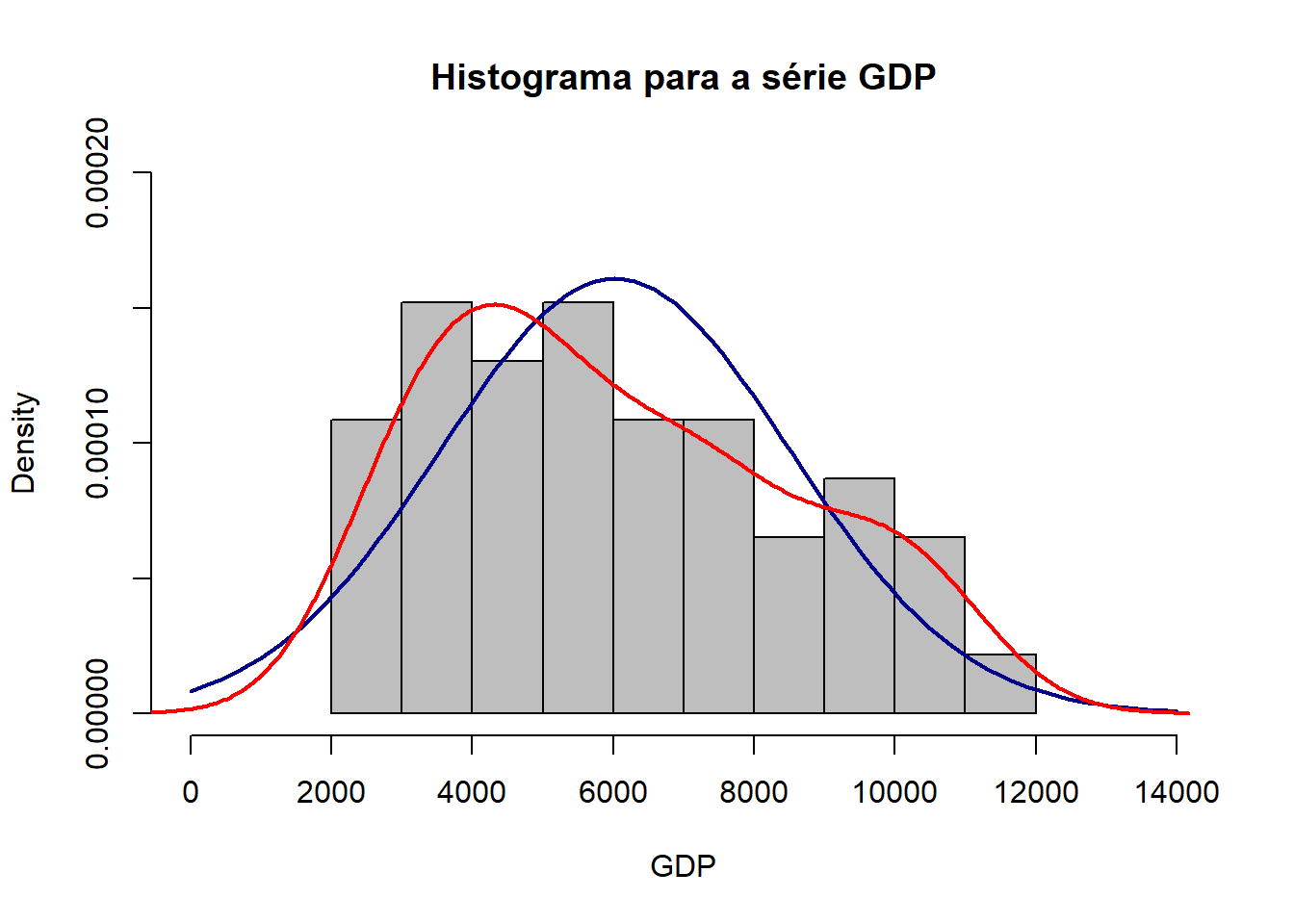
4.2 Correlação entre variáveis
Análises econométricas têm como ideia subjacente que as variávies y e x são relacionadas de alguma forma. Nesse sentido, busca-se explicar quanto y varia dada uma variação em x. Destaca-se que y é denominada variável dependente, variável explicada, variável de resposta, variável prevista ou regressando. Por sua vez, x é conhecida como variável independente, variável explicativa, variável de controle, variável preditora ou regressor. Então, para testar se y e x são relacionadas de alguma forma utiliza-se a análise de correlação.
Os valores da análise de correlação estarão sempre entre \(+1\) e \(-1\) e indicam a relação entre duas variáveis lineares. Em que a magnitude da vairável indica a força da correlação e o sinal indica a direção da relação, se a correlação é positiva ou negativa, i.e., se as variáveis são diretamente proporcionais ou inversamente proporcionais, respectivamente.
## calculando a correlação entre as variáveis do data.frame
cor (pers_con, use = 'complete.obs', method = 'kendall')## year ecp gdp
## year 1.0000000 0.9956502 0.9879170
## ecp 0.9956502 1.0000000 0.9922705
## gdp 0.9879170 0.9922705 1.0000000Uma vez realizada a análise de correlação, pode-se ainda determinar a magnitude da interdependência entre y e x. A estatística covariância é uma medida do grau de interdependência numérica entre duas variáveis. Assim, se duas variáveis são independentes umas das outras espera-se que elas tenham covariância igual a zero. Por sua vez, um sinal positivo indica uma relação linear positiva enquanto um sinal negativo sinaliza uma relação linear negativa.
## [1] 44335974.3 Mínimo Quadrado Ordinário (MQO)
O método do Mínimo Quadrado Ordinário (MQO) é um dos estimadores bastante utilizado em análises econométricas, isto é, em estudos empíricos. O MQO caracteriza-se como sendo uma técnica de otimização matemática em que se procura encontrar o melhor ajuste para um conjunto de dados buscando minimizar a soma dos quadrados das diferenças entre o valor estimado e os dados observados. Salienta-se que o comando para o estimador MQO no R é lm.
## estimando a regressão linear simples entre 'epc' and 'gdp'
reg <- lm (pers_con$ecp ~ pers_con$gdp)
## obtendo o resultado da regressão linear simples entre 'epc' and 'gdp'
summary (reg)##
## Call:
## lm(formula = pers_con$ecp ~ pers_con$gdp)
##
## Residuals:
## Min 1Q Median 3Q Max
## -148.819 -49.780 -5.844 36.780 169.113
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -2.970e+02 2.814e+01 -10.56 1.23e-13 ***
## pers_con$gdp 7.213e-01 4.327e-03 166.70 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 71.96 on 44 degrees of freedom
## Multiple R-squared: 0.9984, Adjusted R-squared: 0.9984
## F-statistic: 2.779e+04 on 1 and 44 DF, p-value: < 2.2e-16## plotando o gráfico para a regressão linear simples entre 'ecp' and 'gdp'
plot (pers_con$gdp, pers_con$ecp)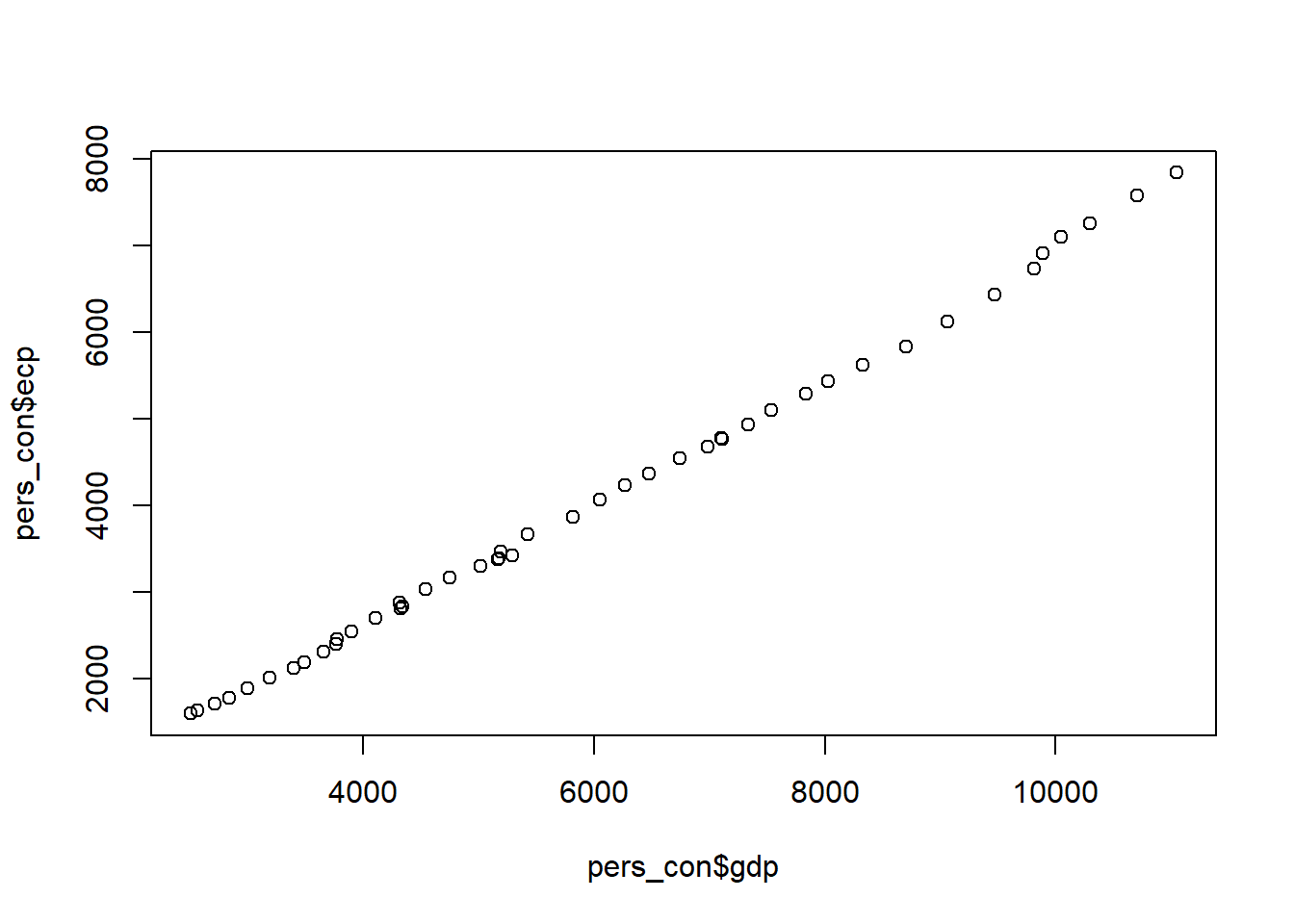
## adicionando a linha da regressão linear simples estimada entre 'ecp' and 'gdp'
## e renomeando os eixos 'x' and 'y'
plot (pers_con$gdp, pers_con$ecp, xlab = 'gdp', ylab = 'ecp')
abline (lm (pers_con$ecp ~ pers_con$gdp), col = 'red', lwd = 2)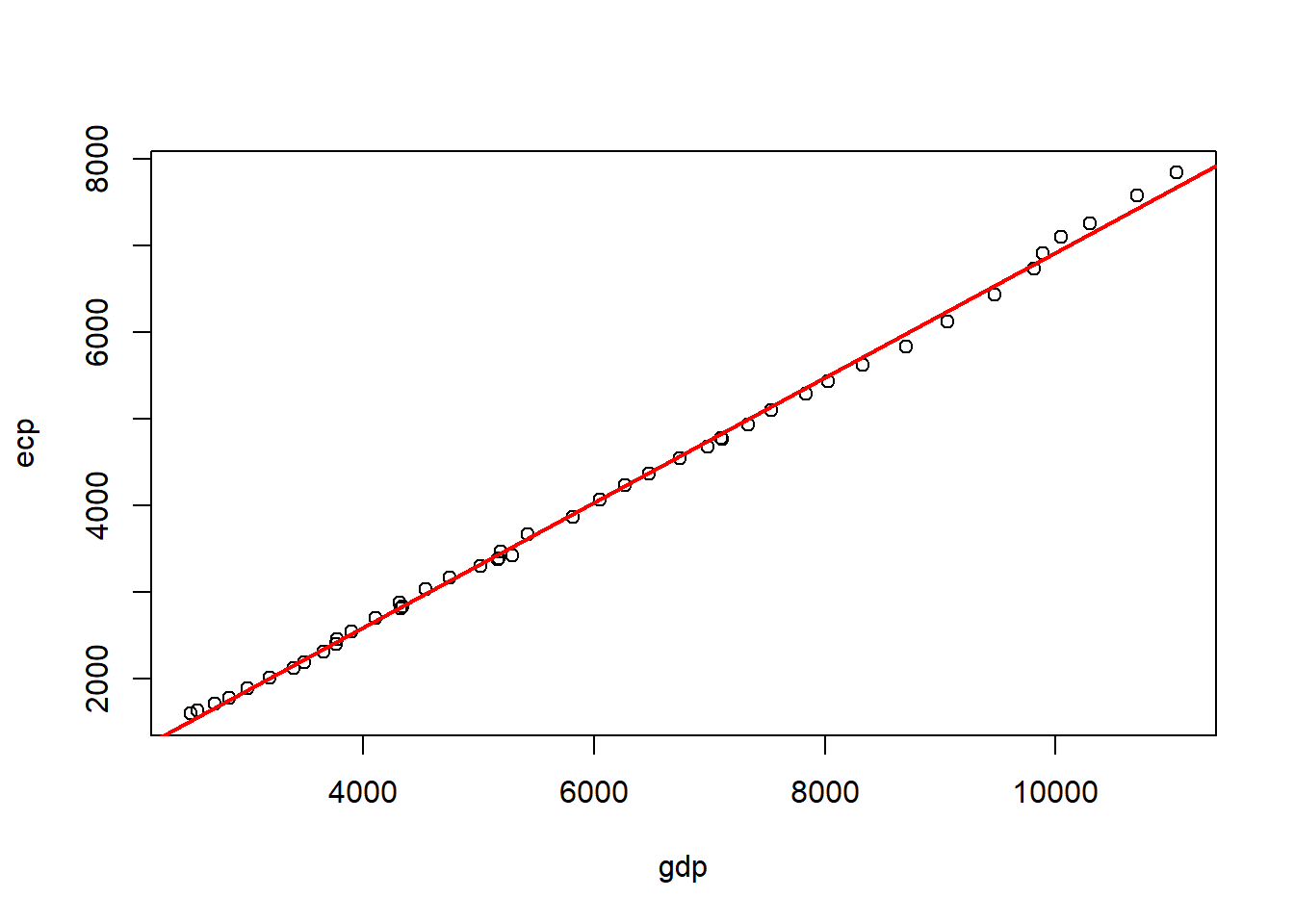
4.4 Teste para forma funcional Reset
Para testar se a forma funcional está correta pode-se usar o teste RESET proposto por Ramsey (1969) e que está disponível no pacote lmtest.
## Warning: package 'lmtest' was built under R version 3.5.3## Warning: package 'zoo' was built under R version 3.5.3##
## RESET test
##
## data: pers_con$ecp ~ pers_con$gdp
## RESET = 28.579, df1 = 1, df2 = 43, p-value = 3.238e-064.5 Obtendo os resíduos e os valores ajustados da regressão
Para obter os resíduos e os valores ajustados pode-se usar os seguintes comandos, respectivamente,
4.6 Teste para a presença de heterocedasticidade
Para testar a presença de heterocedasticidade nos dados aplica-se o teste Breusch-Pagan proposto por Breusch and Pagan (1979) contra a heterocedasticidade disponível no pacote lmtest.
##
## studentized Breusch-Pagan test
##
## data: pers_con$ecp ~ pers_con$gdp
## BP = 20.183, df = 1, p-value = 7.037e-064.7 Interpretando a saída do MQO
O primeiro resultado reportado pela saída de uma estimação empregando o MQO (comando lm) é a forma funcional estimada. Logo após, são apresentadas as estatísticas descritivas dos resíduos: valor mínimo, primeiro quartil, mediana, terceiro quartil e valor máximo. Para uma distribuição normal espera-se que: o valor mínimo e o valor máximo sejam idênticos (porém, com sinais opostos: negativo para o valor mínimo e positivo para o valor máximo) bem como o primeiro quartil deve ser igual ao terceiro quartil (negativo para o primeiro quartil e positivo para o terceiro quartil).
O próximo resultado são os coeficientes (coluna Estimate). O termo Intercept é denominado de constante e representa o ponto em que a linha ajustada da regressão interceptará o eixo vertical do gráfico. Ademais, a inclusão do \(\beta_0\) garante que os resíduos tenham uma média zero. Já o coeficiente gdp indica que con e gdp possuem uma relação positiva, ou seja, ao aumentar a variável gdp (o x) o efeito será de um aumento na variável con (o y), isto é, gdpimpactará positivamente con. Mais precisamente, ao aumetar o gdp em um unidade con aumentará por um valor de \(0,07213\).
A coluna Std. Error apresenta o valor do erro padrão para cada um dos coeficientes estimados medindo a confiabilidade do coeficiente. Quanto menor esse valor maior a confiabilidade dos coeficientes.
A estatística t value mostra o valor da estatística-t tabelada ou teste t das variáveis incluídas na equação cujo objetivo é testar a hipótese do coeficiente ser igual a zero. Por sua vez, a coluna Pr(>|t|) apresenta a probabilidade da estatística-t calculada seja superior à estatística-t tabelada e, assim, o coeficiente ser igual a zero. Ademais, Signif. codes indica o nível de significância de rejeição da hipótese nula de coeficiente igual a zero cujos intervalos são interpretados da seguinte forma:
Reference
Breusch, Trevor S, and Adrian R Pagan. 1979. “A Simple Test for Heteroscedasticity and Random Coefficient Variation.” Econometrica: Journal of the Econometric Society, 1287–94.
Gujarati, Damodar N, and Dawn C Porter. 2011. Econometria Básica. 5th ed. Editora Campus, Rio de Janeiro: Elsevier.
Ramsey, James Bernard. 1969. “Tests for Specification Errors in Classical Linear Least-Squares Regression Analysis.” Journal of the Royal Statistical Society. Series B (Methodological), 350–71.